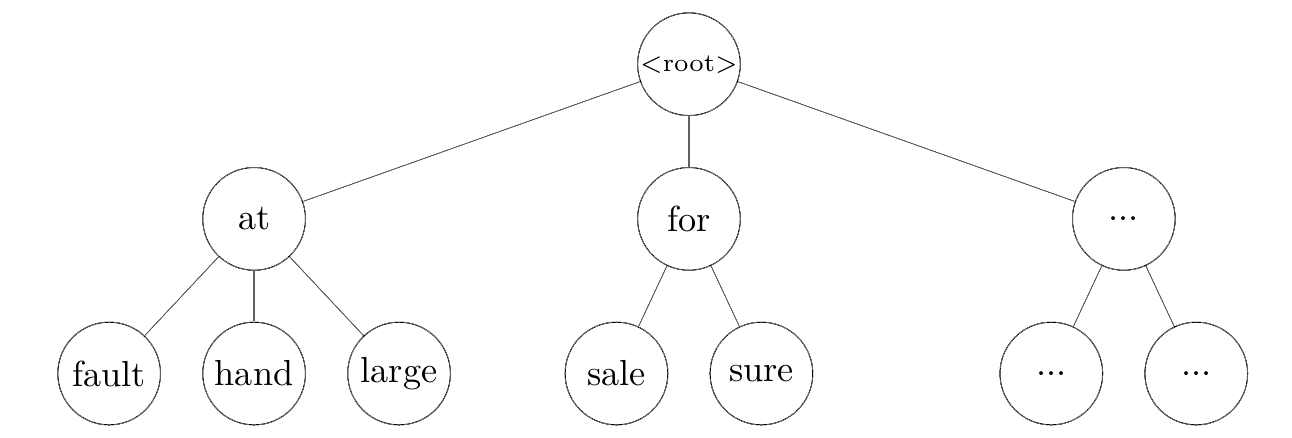
日本語を学んでいく中で特に印象的だったのは、覚えた漢字が一定数を超えると、それまで見たことのない単語でも読めたり意味を推測できたりすることです。これは漢字そのものが意味を持つから可能になることです。たとえば、建物は建つ物、自信は自分を信じること、などのように漢字から意味がわかる単語が少なからずあります。初めて耳にする言葉でも、その漢字を推測して意味に辿り着けることがあります。

英語でも見たことのない単語の意味を推測できる場合はありますが、主に-ness（例：kindness）やre-（例：rewrite）といった生産的な¹接辞か、認識しやすいラテン語由来の語根を持つ単語です。英語において、漢字から推測可能な単語に最も近いのは複合語だと思っています。すべてが推測可能というわけではありませんが、mailbox（郵便箱）、firefighter（消防士）、waterfall（滝）など、わかりやすいものもあります。この話がなぜ大事なのかというと、こういった推測しやすい複合語が多いほど新しい語彙を覚える負担が減るからです。たとえば、エスペラント（最も広く使われている人工言語）は、生産的な接辞と複合語を広範に活用しています（今回話すのは複合語のみですが）。

さて、本題は複合語を自動生成する方法があるかどうかですね。複合語を構成する単語がその複合語の意味と関連している必要があります。同時に、語彙全体も考える必要があります。1つの単語が多くの複合語に使われすぎると、手がかりとしての役割が薄れます。そのため、複数の基準を考慮しながら、最適な複合語語彙を見つける方法が必要になります。

探索問題としての捉え方

まず初めに、単語（複合語を含む）で表現したい意味の集合を考えます。これらを「アイデア」と呼び、英単語で表現します。このアイデアの集合 をIとし、 語彙を構築するプロセスは、I から基礎語の集合 B を選び（B ⊂ I）、I の残りの要素を B の2つの単語を組み合わせた複合語として表現することと考えられます²。これにより、複合語の集合 C が生まれます。C の各要素は、アイデアと2つの基礎語を表すタプルになります：C = { (i, b1, b2) ∣ b1 ∈ B, b2 ∈ B, i ∈ I }。

たとえば、以下のような3つの単語が I に含まれているとします：

sky

water

rain

この場合、最適な結果は sky と water を基礎語に選び、rain を skywater という複合語で表現することだと言えるでしょう。つまり、基礎語の集合は以下のようになります：

B = {sky, water}

そして、それらが組み合わさって以下の複合語の集合が得られます：

C = {(rain, sky, water)}

実際の言語では I が何千、何万といった規模になるため³、これを手作業で行うのは現実的ではありません。しかし、I からB と C を生み出す処理を、Iの要素をBにコピーするかIの要素を表す複合語を作り出すかを順次に選択する長い決定の連続とみなすことができます。決定空間は広大になりますが、自動探索することは可能です。自動探索のためには、結果を評価する基準が必要になります。

たとえば、以下のような関数 S(I, B, C) を評価基準とすることが考えられます：

1. C に含まれる各複合語の質を最大化する
2. 多数の複合語に使用される基礎語の数を最小化する
3. #2を損なわない範囲で可能な限り多くの複合語を作る⁴

私の試み（モンテカルロ木探索）

モンテカルロ木探索（MCTS）のアルゴリズムはゲームAIのものと認識されることが多いと思いますが、評価基準さえあれば決定の連続としてモデル化できるあらゆる問題に適用できます。私は最適化手法の専門家ではないですが、この手法は本プロジェクトに適切であるように思えます。こちらのページにMCTSの概要が掲載されていますので、ここでは基本的な考え方だけ説明します。ただし図があると非常にわかりやすくなってくるので、それだけは借りたいと思います。

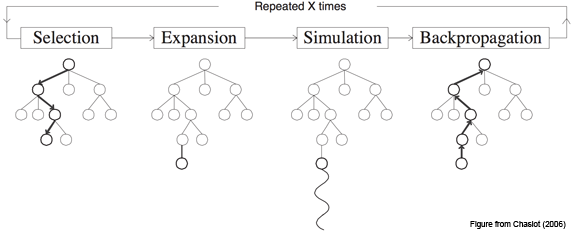
MCTSは、以下の4つのステップを繰り返して行われます：

1. 選択: ルートから始めて、スコアを考慮しながら有望な葉ノードを探します。
2. 展開: その葉ノードに1つの子ノードを生成して追加します。
3. シミュレーション: 完成または深さの最大値に至るまでノードの生成を繰り返し、上記の子ノードの仮サブツリーを構築してスコアします。
4. 逆伝播: スコアを根ノードまで伝播します。

理論上、良い評価関数があり、かつハイパーパラメータをうまく調整して探索と活用のバランスを取れれば、MCTSは高得点の状態（結果）に至るパスを見つけてくれます。本プロジェクトでその高得点の状態というのは、パスにある各ノードで行われた選択に構造された複合語の語彙です。

実装の複雑さを抑えるため、今回は複合語の選択と作成の最適化だけを目指し、生成される複合語の目標数を Iのサイズの一定割合に固定しました。つまり、前節の基準で挙げた#1（複合語の質）と#2（基本語の使用過多を最小化）のみを最適化対象としました。なのでMCTSツリーの各ノードは、未使用のアイデアを1つ選択し、2つの基本語を選択して組み合わせ、それによって得られる複合語をCに追加する操作を表すことになりました。

複合語の生成と評価

生成される複合語がそのアイデアと意味的に関連する単語で構成されるように、ConceptNet 用いて候補単語を集める手法を取りました。ConceptNet は、英単語のノードを意味的な関係を表すエッジで結ぶ知識グラフです。アイデアの英単語に接続されたエッジをたどって基本語を探すことで、複合語が表すアイデアとそれを構成する単語の間に何らかの意味的な関係があることを保証できます。理論上はこれでfirefighter のようなわかりやすい言葉を目指し、honeymoon のような直感的ではない複合語を避けられます。

具体的には、アイデアがランダムに I から選ばれ、ConceptNetで収集された候補の中から I にも含まれる単語がランダムに複合語を構成する基本語として選ばれて複合語が生成されます。このときに選ばれた単語は B に追加されます。展開とシミュレーションの際にスコアを活用して子ノードを選ぶ方法も試しましたが、処理速度が大幅に低下しました。また、理論上スコの計算をシミュレーション後にのみ行っても、逆伝播が各ノードのスコアを調整してくれるので、そうさせてもらいました。

複合語の評価関数の開発だけでも中々の難題なので、今回は最もシンプルな方法を取り、アイデアを表す単語と構成する基本語の単語ベクトル間のコサイン類似度を評価関数として利用しました。スコアは次の式で計算されます：
score(compound) = (similarity(b1, i) + similarity(b2, i) + relationScore) / 3
ここで、relationScore は ConceptNet における関係の種類ごとに手動で設定された値です（例：x is a y は x desires y より高スコア）。

MCTSの評価関数（スコアリング）

MCTSで使用する評価関数は、特定のノードや複合語ではなくツリーを下る経路によって得られる状態を評価するものになります。この場合、状態とは生成された複合語集合 C と、各基本語の使用回数の2つを指します。上述の基準#1（複合語の質）と#2（基本語の使用過多を最小化）を最適化するため、各複合語のスコアの合計を基本語の使用回数の二乗和で割った値をスコアとしました。

結果

これまでの説明から明らかだと思いますが、動作するプロトタイプにたどり着くためにいくつか手を抜きました。スコアリング関数がかなり適当だったことに加え、ノートPCの計算能力では MCTS の反復を十分に回せなかった結果、問題に対する良い解決策と呼べるものにはなりませんでした。とはいえ、いくつか共有する価値のある出力が得られたと思います。こちらにコードを公開しているので、興味のある方はより良い方法に挑戦してみてください。

出力例

以下は実際に生成された結果の一部です（厳密に言えば組み合わせは順序なしです）：

• segment + year = month
• crime + theft = robbery
• beach + edge = shore
• act + wedding = marriage
• cry + vegetable = onion
• computer + storage = disk
• air + crime = pollution
• bottom + dress = skirt

上記の例の中に、結婚を意味するact + weddingのようにやや抽象的な組み合わせもありますが、我ながらcry + vegetableが玉ねぎの意味になっているのはかなり良かったです。しかしここで重要なのは、どの例の複合語も表しているアイデアに合った組み合わせになっています。玉ねぎは人を泣かせる野菜だし、segment + yearになった月を意味する複合語も1年の一部です。とはいえ、出力の大半はそれほどうまく行っていません。失敗例もいくつか記載します。

• class + senior = freshman
• kitchen + meal = cook
• chicken + male = hen

多くの出力と同じくこれらの3語は、アイデアの単語と似ている文脈に出てくるがそのアイデアを表すには良くない単語に構成されています。これはまさに単語ベクトル（分散意味論）に基づいた評価関数を用いたせいです。全出力はこちらにあります。

最後に

MCTSを用いて複合語を生成するしっかりした実装や優れた評価関数の開発は、それ自体で研究論文になり得ます。ちゃんとしたものにするにはせめて以下が必要でしょう：

• 優れた複合語の評価関数
• 複合語として表現されるアイデアの数も探索可能なMCTSの実装
• 大量の計算資源

さらに、次のような要素もあった方がよいかもしれません：

• MCTSでの子ノード生成を賢くする評価関数（完全にランダムより良い方法）
• ConceptNet以外の、アイデアと意味的関係のある単語を探せるデータ源

本プロジェクトを論文レベルまで引き上げるつもりはありませんが、人工言語の構築に役立つ可能性のある面白いプロジェクトだと思います。もしこの取り組みをさらに発展させたい方がいれば、遠慮なくご連絡ください。

---

最近、文中の複数語表現（MWE）の見つけ方について考えるのにかなりの時間をかけています。MWEの定義は曖昧で、定義次第で何がMWEに該当するかが変わりますが、今日はその点は置いておき、MWEの自動検出について説明します。

MWE検出の方法はさまざまですが、個人的には辞書ベースのものが好きです。簡単に言うと、MWEがたくさんあるリストが与えられ、そのうちのどれが文中に実際にあるかを割り出す手法です。これは以下のようなパイプラインとして表現できます：

1. 文中に存在し得るMWE（「可能なMWE」）を辞書から検索します。これは、辞書データから構成素がすべて文中にあるMWEを抽出する処理として考えることができます。辞書がうまく構造化されていないとかなり遅くなるので、本記事の大半はこの処理を効率化する方法の説明になります。
2. 検索された可能なMWEを構成し得る構成素の組み合わせを全て文中から「候補」として集めます。単純に可能なMWEに相当する単語の各組み合わせを見つける処理になりますが、記事の最後に説明します。
3. 各「候補」が実際にMWEであるかどうかを判断します。つまり、その構成素が慣用的/非構成的な意味を持つかどうかです。こうするには文脈における意味を判断できるシステムが必要であり、たいていの場合は機械学習に基づいた手法になります。昨年その方法の1つについて論文を出版しましたが、この記事で詳しく解説するには手法が多くて複雑すぎます。

上記の文に対して、この3つのステップは以下のようになります：

1. run_down, run_over, fall_down, fall_overを検索して可能なMWEとして取得します。これらの4件は、辞書から構成素がすべて文中に含まれているMWEのすべてです。
2. これらのMWEを文中の単語の組み合わせに対応付け、上図で描写されているように候補を見つけます。
3. 候補をフィルタにかけ、実際にMWEの意味になっている候補に絞り込みます。fall_downとrun_overは明らかに間違っており、run_downというMWEは「（車両で）人をひく」のような意味なので、fall_overだけが残ります。

1つのMWEに対して候補の単語組み合わせが複数ある場合もあります。たとえば、最後のdownをoverに置き換えて「I ran down the stairs and fell down」にすると、run_downの構成し得る組み合わせが2つあります。1つ目はranと最初のdownであり、2つ目はranと二番目のdownです。この問題に対応しやすくするためにも、ステップ＃1と＃2を分割して行うのがおすすめです。

可能なMWEの検索

さて、主題のステップ＃1である可能なMWEの検索について説明しましょう。MWEの中に、その出現に制約があるものもありますが、動詞のMWEも考慮に入れると汎用的な制約がほとんどありません。まずShe put her beloved dog downのput_downのように、構成素が連続している必要はありません。さらにthe beans have been spilledのspill_the_beansのように、順序さえ保証されていません。最後に、MWEの構成素が重複しないとも限りません。その例としてface_to_faceなどがあります。

構成素が順序に従う必要がなく、重複しない保証もないことを考えると、可能なMWEの検索という問題は次のように形式化できます。入力文の単語の多重集合Sと、可能なMWEごとの多重集合を含む集合Lが与えられた場合、Sの部分集合でありかつLに含まれる要素を見つけることです。

その結果、MをMWEごとの多重集合の平均要素数とし、最悪計算量は*O(M * |L|)*というかなりひどい上限になります。辞書内の各MWEが文中の単語の部分集合であるか否かを調べる単純な手法だと、各文ごとに全てのMWE多重集合を処理することになってしまうので、非常に遅くなります。

class NaiveApproach:
    def __init__(self):
        self.data = [
            (mwe['lemma'], Counter(mwe['constituents']))
            for mwe in get_mwes()
        ]

    def search(self, words: list[str]) -> list[str]:
        word_counter = Counter(words)
        return [
            mwe for mwe, constituents in self.data
            if all(
                word_counter[constituent] >= count
                for constituent, count in constituents.items()
            )
        ]

このコードは私のノートパソコンで1,000文を処理するのに平均して28秒かかります。しかし、トライ木を使用することで大幅に高速化できます¹。トライ木は通常、文字から構築されるものですが、この場合は文字ではなくて単語を扱っているため、単語から構築します。

MWEのトライ木を辞書として使用すると、深さ優先探索で可能なMWEを集めることができます。この探索は、文中にない単語のノードに突き当たったところで中断します。つまり、文中の単語の部分集合であるトライ木の部分のみをたどることができます。

class TrieNode:
    __slots__ = ['lemma', 'children']

    def __init__(self, lemma: Optional[str]):
    	# lemma represents a possible MWE that terminates at this node
        self.lemma = lemma  
        self.children = {}


class Trie:
    def __init__(self):
        self.tree = self._build_tree(get_mwes())

    def _build_tree(self, mwes: list[dict[str, str]]):
        root = TrieNode(None)
        for mwe in mwes:
            curlevel = root
            for word in mwe['constituents']:
                if word not in curlevel.children:
                    curlevel.children[word] = TrieNode(None)
                curlevel = curlevel.children[word]

            curlevel.lemma = mwe['lemma']

        return root

    def search(self, sentence: list[str]) -> list[str]:
        counter = Counter(sentence)
        results = []
        self._search(self.tree, counter, results)
        return results

    def _search(self, cur_node: TrieNode, counter: Counter, results: list):
        possible_next_constituents = [c for c in counter if counter[c] > 0 and c in cur_node.children]

        for constituent in possible_next_constituents:
            next_node = cur_node.children[constituent]
            counter[constituent] -= 1
            if next_node.lemma is not None:
                results.append(next_node.lemma)
            self._search(next_node, counter, results)
            counter[constituent] += 1

これで辞書内のMWE間で共有される接頭辞を一つだけ保存できるようになりますが、主な利点は上記のように検索を行うことで、最初の単語が文中に含まれないMWEに対して計算資源を一切費やさないことです。こうするとかなり早くなり、1,000文を平均で0.8秒で処理できます。しかしもう少し早くすることはまだ可能です。

英語の単語出現頻度は大きく偏っており、出現頻度の高い単語から始まるMWEも多いです。この実験で使用した比較的に小さい辞書でも、inから始まるMWEが169件もあります。たとえばin_theory, in_unison, in_vain, などがあります。構成素が全て文中にあるMWEしか求めていないため、出現の可能性が最も低い単語の有無を最初に調べた方が効率が良いはずです。つまり、一番出現頻度の低い単語から処理するということです。トライ木に入れる前に、出現頻度のデータを用いてMWEの構成素を出現頻度の低い順に並び替えることでこういった検索を実現できます。注意点としては、単語を共有して順序だけで区別されるMWEを扱う場合（例えばroast_porkやpork_roast）には、トライ木の1つのノードに複数のMWEを結びつける必要がありますが、わずかな変更で済みます。

class OrderedTrie:
    # not pictured here: 
    # 1) TrieNode now holds a list of lemmas instead of a single lemma
    # 2) _search needs one line changed to return all lemmas on a node 

    def __init__(self, word_data: dict[str, int]):
        # any missing words are treated as last in the frequency list
        self.word_freqs = defaultdict(lambda: len(word_data), word_data)
        self.tree = self._build_tree(get_mwes())

    def _reorder(self, words: list[str]) -> list[str]:
        # sort by word frequency, then alphabetically in case
        # both words are missing from word_freqs
        return sorted(words, key=lambda w: (self.word_freqs[w], w), reverse=True)

    def _build_tree(self, mwes: list[dict[str, str]]):
        root = OrderedTrieNode([])
        for mwe in mwes:
            curlevel = root
            for word in self._reorder(mwe['constituents']):
                if word not in curlevel.children:
                    curlevel.children[word] = OrderedTrieNode(word)
                curlevel = curlevel.children[word]

            curlevel.lemmas.append(mwe['lemma'])

        return root

この並び替えた構成素のトライ木の手法を使うと、平均でたった0.5秒で1,000文を処理することができ、前述のトライ木より４割程度早くなります。各種法の平均処理時間は以下のグラフに表示されています（対数スケール）。

単純な検索手法からトライ木に基づいた手法に切り替えることは割と明白な改善と言えますが、ここで興味深いのはトライ木の構造を単語の頻出度で最適化することによる高速化だと思います。なにより、処理しようとしているデータやドメインを理解する重要性の示す良い例でしょう。このさらなる高速化は英文の単語である入力データの分布を考えて初めて可能になるものです。

検索された可能なMWEと候補の単語組み合わせの対応付け

これで可能なMWEを検索する方法はわかったので、特定のMWEを構成し得る単語の組み合わせを文中から全て見つけるステップ#2を簡単に見てみましょう。文I ran down the stairs and fell downとMWErun_downの場合、まず文をトークン列として、MWEを多重集合として表現できます。

from collections import namedtuple, defaultdict
from itertools import combinations, product

token = namedtuple("Token", ["form", "idx", "lemma"])
sentence = [
    token("I", 0, "I"),
    token("ran", 1, "run"),
    token("down", 2, "down"),
    token("the", 3, "the"),
    token("stairs", 4, "stairs"),
    token("and", 5, "and"),
    token("fell", 6, "fall"),
    token("down", 7, "down"),
    token(".", 8, "."),
]

# build a map of lemmas to tokens
# so we can look up tokens by their lemma
lemma_to_tokens = defaultdict(list)
for t in sentence:
    lemma_to_tokens[t.lemma].append(t)

# mwe: "run_down"
lemma_counter = {
    "run": 1,
    "down": 1,
}

以下のコードは一見では分かりづらいかもしれませんが、やっていることはそれほど複雑ではありません。MWEに含まれる各見出し語に選べるトークンをタプルとして表現し、可能な選択肢を全て集めます。ちなみにこれは各見出し語に対してN語からK語を選ぶ組み合わせを求めることに相当します。ここで、Nはその見出し語が文中に出現する回数であり、Kはその見出し語がMWEに出現する回数になります。得られたタプルには、通常の場合は1つの要素しか含まれませんが、face_to_faceのように同じ構成素が繰り返されるMWEでは複数の要素が含まれることがあります。

candidate_word_combos = [
    list(combinations(lemma_to_tokens[lemma], lemma_counter[lemma]))
    for lemma in lemma_counter
]

上記のコードを走らせると、以下の結果が得られます。

[
    [
        (Token(form='ran', idx=1, lemma='run'),)
    ], 
    [
        (Token(form='down', idx=2, lemma='down'),), 
        (Token(form='down', idx=7, lemma='down'),)
    ]
]

最後に、これらのタプルのリストごとに直積集合を取り、タプルを展開（アンパック）します。各タプルは見出し語にトークンを選ぶ方法を表現しているので、これは実質的に各見出し語に対して単語の選び方の組み合わせを全て検討することになります。それはつまり、元々の目的である、特定のMWEを構成し得る単語の組み合わせを得ることができます。仕上げに、結果に含まれるトークンの順番を直します。

mwe_combinations = {
    tuple(x for y in p for x in y) 
    for p in product(*candidate_word_combos)
}

sorted_mwe_combinations = [
    sorted(raw_combo, key=lambda t: t.idx) 
    for raw_combo in mwe_combinations
]

そして最終結果が以下となります。

[
    [
        Token(form='ran', idx=1, lemma='run'), 
        Token(form='down', idx=2, lemma='down')
    ], 
    [
        Token(form='ran', idx=1, lemma='run'), 
        Token(form='down', idx=7, lemma='down')
    ]
]

 

---

私が現在所属している生産技術研究所は、2ヶ月に1回生研ニュースという広報誌のようなものを出版していますが、4月号の「PROMENADE」という海外から来ている研究員が書く枠の記事を執筆しました。日本語で執筆と言えるようなものは初めてなので、記念に保管しておきたいと思いました。主に来日とそれからの生活の話ですが、記事に載っている「生研ニュース#189」へのリンクは下に載せているのでもし興味があれば読んでみてください。

ちなみに、記事の文頭に出てくることわざは日本語とイディッシュ語（東欧のユダヤ人の言語）で書いていますが、実は英語で「Man makes plans and god laughs」として親に教えてもらったもので、この記事の下調べで初めてそれがイディッシュ語のことわざだと知りました。ご先祖様が東欧ユダヤ人なのはもちろん知っていましたが、普段から使っている英語にイディッシュ語の直訳があることに驚き、少しだけ自分のルーツを感じました。

記事はここで閲覧できます