I've recently spent quite a bit of time thinking about how to find multiword expressions (MWEs) in a sentence. MWEs are a pretty messy topic and there is a lot of ambiguity about what even counts as an MWE, but for today I want to put that aside and talk about approaches to automatically identifying MWEs. I am a fan of lexicon-based approaches to MWE identification, which just means that given a very large list of MWEs, you are trying to figure out which of them might be present in a given sentence. This can be broken down into a pipeline that looks something like this:

1. Retrieve all of the MWEs that could be present in a sentence (the "possible MWEs") from the lexicon; this can also be thought of as filtering the lexicon down to just entries whose constituents are all present in the sentence. The majority of this blog post will be about how to do this efficiently, because with a poorly structured lexicon this can be quite slow.
2. Gather all combinations of constituent words which could form a possible MWE in the sentence as "candidates"; this just means finding each combination of words in the sentence that correspond to a possible MWE. We will cover how to do this at the end of the post.
3. Decide if each "candidate" is actually an MWE - that is, whether its constituents take on an idiomatic/non-compositional meaning. This requires a system capable of making judgements about meaning in context, which typically means machine learning. I published a paper last year about one possible method to do this, but there are a variety of possible approaches, which are beyond the scope of this blog post.

For the above sentence, these three steps look like this:

1. Retrieve run_down, run_over, fall_down, fall_over as possible MWEs - this is every MWE in our lexicon with all of its constituents present in the sentence.
2. Find candidates for these MWEs by mapping each of them to groups of words in the sentence, as pictured in the above diagram.
3. Filter these so that we keep only the candidates whose meaning is that of the relevant MWE. fall_down and run_over are obviously wrong, and run_down as an MWE means something like (of a vehicle) to hit a person and knock them to the ground, so we are left with fall_over.

Note that there are sometimes multiple candidate word groups for a single MWE. For example, if we replace the last down with over for I ran down the stairs and fell down, there are now two combinations of words that can form run_down - one for ran and the first down, and another for ran and the second down. This is also why it is convenient to split step #1 and #2 into separate steps.

Retrieving possible MWEs

Now, the main topic: retrieving possible MWEs for step #1. While some MWEs have constraints on how they can be formed in a sentence, if we include verbal MWEs then there are very few guarantees. They do not have to be contiguous - see put_down in She put her beloved dog down - and worse, they do not even have to be in order - see the beans have been spilled for spill_the_beans. Finally, the constituent words of an MWE are not always unique, such as in face_to_face.

Given that constituent words are neither required to be in order nor unique, the formalization of our possible MWE retrieval problem is: given a multiset S of words in the input sentence, and a set L containing multisets for each possible MWE, find all members of L that are strict subsets of S.

This means a worst case runtime of O(M * |L|) where M is the average size of an MWE multiset, which is a pretty expensive upper bound. The naive approach of checking if every MWE in the lexicon is a subset of the words in the sentence will end up processing every MWE multiset for every sentence, and is consequently very slow.

class NaiveApproach:
    def __init__(self):
        self.data = [
            (mwe['lemma'], Counter(mwe['constituents']))
            for mwe in get_mwes()
        ]

    def search(self, words: list[str]) -> list[str]:
        word_counter = Counter(words)
        return [
            mwe for mwe, constituents in self.data
            if all(
                word_counter[constituent] >= count
                for constituent, count in constituents.items()
            )
        ]

This code takes an average of 28 seconds on my laptop to process (call search() on) 1,000 sentences. Fortunately, we can make this much faster using a trie¹. Tries are prefix trees most commonly built out of characters, but because we are dealing with words and not characters, we will build ours out of words.

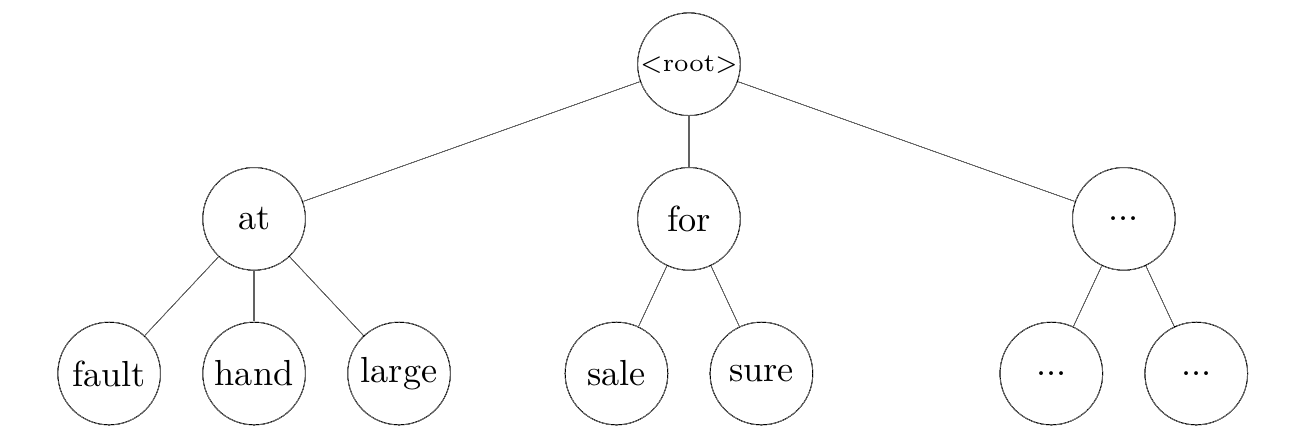
Using the MWE trie as our lexicon, we can gather possible MWEs with a depth-first search starting at the root, which aborts when we hit a node for a word missing from the sentence. That is, we can traverse only the parts of the trie that are subsets of the words in the sentence.

class TrieNode:
    __slots__ = ['lemma', 'children']

    def __init__(self, lemma: Optional[str]):
    	# lemma represents a possible MWE that terminates at this node
        self.lemma = lemma  
        self.children = {}


class Trie:
    def __init__(self):
        self.tree = self._build_tree(get_mwes())

    def _build_tree(self, mwes: list[dict[str, str]]):
        root = TrieNode(None)
        for mwe in mwes:
            curlevel = root
            for word in mwe['constituents']:
                if word not in curlevel.children:
                    curlevel.children[word] = TrieNode(None)
                curlevel = curlevel.children[word]

            curlevel.lemma = mwe['lemma']

        return root

    def search(self, sentence: list[str]) -> list[str]:
        counter = Counter(sentence)
        results = []
        self._search(self.tree, counter, results)
        return results

    def _search(self, cur_node: TrieNode, counter: Counter, results: list):
        possible_next_constituents = [c for c in counter if counter[c] > 0 and c in cur_node.children]

        for constituent in possible_next_constituents:
            next_node = cur_node.children[constituent]
            counter[constituent] -= 1
            if next_node.lemma is not None:
                results.append(next_node.lemma)
            self._search(next_node, counter, results)
            counter[constituent] += 1

This allows us to store only a single copy of any prefixes shared between multiple MWEs in our lexicon, but the main benefit is that searching this way means we will expend no compute on MWEs whose first word is not present in the sentence. This is much faster, and gets through 1,000 sentences in 0.8 seconds on average. However, we can still make it a little faster.

Word frequency in English is very imbalanced, and many MWEs start with common words. For example, my relatively small lexicon has 169 MWEs starting with in, such as in_theory, in_unison, in_vain, etc. Since we only want MWEs whose constituents are all present in the sentence, it makes more sense to look at the words least likely to be present first - that is, the lowest frequency words. We can do this by sorting the constituent words in the MWEs before we insert them into the trie using precomputed word frequency, such that the lowest frequency words come first. This does mean that in rare cases where MWEs share the same words and are differentiated only by order (like roast_pork and pork_roast) we will need to attach multiple MWEs to one node in the trie, but this requires only minor changes.

class OrderedTrie:
	# not pictured here: 
    # 1) TrieNode now holds a list of lemmas instead of a single lemma
    # 2) _search needs one line changed to return all lemmas on a node 

    def __init__(self, word_data: dict[str, int]):
    	# any missing words are treated as last in the frequency list
        self.word_freqs = defaultdict(lambda: len(word_data), word_data)
        self.tree = self._build_tree(get_mwes())

    def _reorder(self, words: list[str]) -> list[str]:
        # sort by word frequency, then alphabetically in case
        # both words are missing from word_freqs
        return sorted(words, key=lambda w: (self.word_freqs[w], w), reverse=True)

    def _build_tree(self, mwes: list[dict[str, str]]):
        root = OrderedTrieNode([])
        for mwe in mwes:
            curlevel = root
            for word in self._reorder(mwe['constituents']):
                if word not in curlevel.children:
                    curlevel.children[word] = OrderedTrieNode(word)
                curlevel = curlevel.children[word]

            curlevel.lemmas.append(mwe['lemma'])

        return root

Using this sorted constituent trie approach, it takes only 0.5 seconds on average to process 1,000 sentences, which is about a 40% speedup over the aforementioned trie. The average time for each of the three methods can be seen in the graph below (log scale).

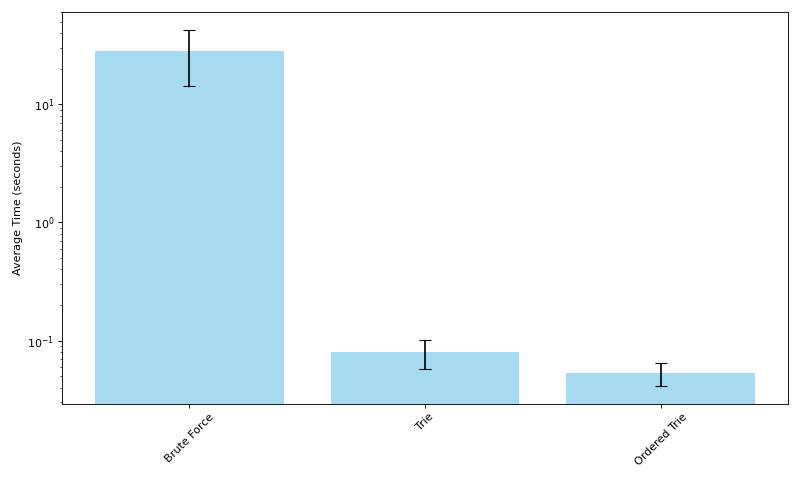
Moving from the naive approach to using a trie is arguably a fairly obvious optimization; I think the interesting part is the further speedup we get from using word frequency to inform trie construction. Most importantly, it's also a good demonstration of how much it can help to have a good understanding of the data/domain you are trying to process. This further speedup was only made possible by thinking about what the distribution of the input data (words in English sentences) looks like.

Mapping retrieved possible MWEs to candidate word groups

Now that we know how to retrieve our possible MWEs, let's look briefly at step #2: finding every combination of words in the sentence that could constitute a given MWE. For the sentence I ran down the stairs and fell down and the MWE run_down, we start by building simple representations of our sentence as tokens and our MWE as a multiset.

from collections import namedtuple, defaultdict
from itertools import combinations, product

token = namedtuple("Token", ["form", "idx", "lemma"])
sentence = [
    token("I", 0, "I"),
    token("ran", 1, "run"),
    token("down", 2, "down"),
    token("the", 3, "the"),
    token("stairs", 4, "stairs"),
    token("and", 5, "and"),
    token("fell", 6, "fall"),
    token("down", 7, "down"),
    token(".", 8, "."),
]

# build a map of lemmas to tokens
# so we can look up tokens by their lemma
lemma_to_tokens = defaultdict(list)
for t in sentence:
    lemma_to_tokens[t.lemma].append(t)

# mwe: "run_down"
lemma_counter = {
    "run": 1,
    "down": 1,
}

The next part is confusing to look at, but what we're doing isn't actually that complicated. We represent tokens choices for each lemma in the MWE as lists of tuples, and want to gather all possible options. This is just N choose K for each lemma, where N is the number of times the given lemma appears in the sentence and K the number of times it appears in the MWE. These tuples will usually be only one element, except in MWEs that have repeated constituents such as face in face_to_face.

candidate_word_combos = [
    list(combinations(lemma_to_tokens[lemma], lemma_counter[lemma]))
    for lemma in lemma_counter
]

Running this on our example input gives us:

[
    [
        (Token(form='ran', idx=1, lemma='run'),)
    ], 
    [
        (Token(form='down', idx=2, lemma='down'),), 
        (Token(form='down', idx=7, lemma='down'),)
    ]
]

Finally, we take the cartesian product of each of these lists of tuples, and unpack the tuples. Because each tuple represents possible ways of choosing tokens for given lemma, this is effectively looking at all combinations of ways to choose words for each lemma, and gives us our original objective - every combination of words that could constitute this MWE. To finish, we sort the results to make sure that the resulting tokens are in order.

mwe_combinations = {
    tuple(x for y in p for x in y) 
    for p in product(*candidate_word_combos)
}

sorted_mwe_combinations = [
    sorted(raw_combo, key=lambda t: t.idx) 
    for raw_combo in mwe_combinations
]

The final result:

[
    [
        Token(form='ran', idx=1, lemma='run'), 
        Token(form='down', idx=2, lemma='down')
    ], 
    [
        Token(form='ran', idx=1, lemma='run'), 
        Token(form='down', idx=7, lemma='down')
    ]
]

 

---